TLDR: I consider replacing reward in the human preference model in RLHF with preference distribution over trajectories. This formulation seems related to the now popular DPO family algorithms, which I will do a deep dive in another post. Fun fact this post was originally uploaded 2 days before DPO was uploaded to Arxiv.

Reinforcement Learning From Human Feedback (RLHF) has taken the AI field by the storm. I became aware of RLHF and more broadly the AI safety and alignment field mid-2022 and got very interested. Most likely due to recency bias, it seemed to be evolving at an extremely fast pace at first (I mean RLHF as a hot topic and technology), which made me write this toy example. Then, after the first quarter of 2023, it seemed all of a sudden have slowed down.

One impression I had about RLHF is that it has mostly focused on scaling. Many efforts were directed to simplifying the process, for example by shifting into a batch rather than continuous human-model interaction process and pay a ton of contractors to labels the data, or by improving language modeling to excel its capability as a chatbot. However, and most likely due to my own ignorance, not as much attention has been paid to designing better model of humans. The most popular type of RLHF uses a very simple human model to translate reward into human labler’s preferences. However, humans can have uncertain, varying, and biased perception and value that depend on large number of socialtechnical factors. In Sebastian Raschka’s alignment reading list, most papers used highly exploratory and iterative process to figure out the researchers’ preferences, communicate them to the lablers, and designing protocols and softwares to make sure that they are consistent over the entire labeling process. Can some parts of this process be automated or the burden be translated to the reward learning step, for example by building better models of humans? The goal here is of course not to actually find a cost-saving method but simply to conduct a thought experiment for the pleasure of scientific understanding as an armchair philosopher.

Two central characteristics I like to think of humans are that 1) every individual is different with their own values, and 2) individuals have their own and most likely inaccurate and biased perception of the world, because we see the world through first-person view rather than bird’s eye view. When we as humans make inference about the motivation behind someone’s behavior, we do keep these ideas in mind rather than assuming every individual has the exact same value and a perfect understanding of the world. This is the idea of Theory of Mind: the process of inferring the mental state of others upon observing their behavior.

A related field to RLHF is Inverse Reinforcement Learning (IRL), which focuses on extracting human reward from behavior instead of preferences. Similar to the current state of RLHF, early IRL also focused purely on retrieving a single reward assuming the person generating the behavior had perfect knowledge of the environment. Thanks to the cross-pollination between IRL, psychology, and human-computer interaction, more nuanced human models have been developed. One of my favorite example is a study which found that human video game players tend to perceive certain game at a lower speed than it actually is using an IRL model. Then they significantly improved human performance by designing a system which corrects for the biased perception.

Can we build such models in to the RLHF pipeline?

Bayesian Theory of Mind

Bayesian theory of mind is a Bayesian model which casts the theory of mind process as Bayesian inference of an agent’s mental state upon observing their behavior. The mental state is represented by a model of agent preference (e.g. a reward function \(R(s, a)\)) and a model of agent beliefs, (e.g., its model of the world \(\hat{P}(s'|s, a)\)). Let’s say they are both parameterized by \(\theta\). We also need to assume the belief and desire are related by a notion of rationality, for example the agent is a Markov Decision Process solver who chooses actions according to a policy \(\hat{\pi}(a|s; \theta)\) proportional to the exponential of expected value for some planning horizon \(H\):

$$ \begin{align} \log\hat{\pi}(a|s; \theta) \propto \mathbb{E}_{\hat{P}_{\theta}, \hat{\pi}}\left[\sum_{t=1}^{H}R_{\theta}(s_t, a_t)\bigg|s_1=s, a_1=a\right] \end{align} $$

Suppose we observe agent behavior in the form of state-action trajectories \(\tau=(s_{1:T}, a_{1:T})\) in an environment, we can infer the agent’s mental state using Bayesian inference:

$$ \begin{align} P(\theta|\tau) &\propto P(\tau|\theta)P(\theta) \\ &= \prod_{t=1}^{T}\hat{\pi}(a|s; \theta)P(\theta) \end{align} $$

where \(P(\theta)\) is a prior over likely agent parameters. Note that the agent’s model \(\hat{P}_{\theta}\) may not be equal to the true environment; the agent is only acting rationally with respect to it’s own model of the environment. This is the key property that leads to flexible inference of nuanced humans. By accounting for the possibility of biased world model, we have the potential to estimate their reward more accurately. It should be noted that the prior also plays a crucial role to avoid degenerate inference, but that is a more nuanced discussion (see this paper). Lastly, we can easily account for individual difference under the Bayesian framework using hierarchical models.
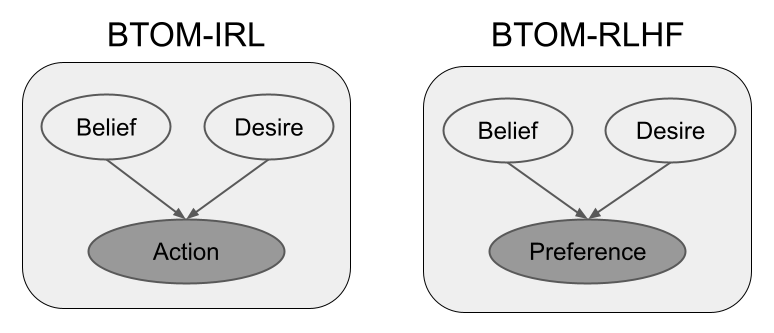Comparison of BTOM for IRL and RLHF.

Bayesian Theory of Mind for RLHF

Let’s consider a simple RLHF scenario where we present to a human evaluator two trajectories \(\tau_{a}\) and \(\tau_b\) and we ask the evaluator to choose a preferred one. This setting can be more advantageous than IRL or Bayesian Theory of Mind because the human does not need to demonstrate optimal behavior which requires substantial skills but simply choose among automatically generated ones which can be produced endlessly.

The key of RLHF is how to model the human evaluator’s choices; or more precisely, the decision process that led to those choices. Most exisiting RLHF uses a simple choice model; although highly effective, perhaps has not fully explored the potential of this framework. Let us denote the information presented to the human as \(x=\{\tau_a, \tau_b\}\) and the choice as \(c \in \{\tau_a, \tau_b\}\), the choice model proposed by one of the earliest RLHF paper and widely in use today is of the following form:

$$ P(c=\tau_a|x; \theta) = \frac{\exp(R_{\theta}(\tau_a))}{\exp(R_{\theta}(\tau_a)) + \exp(R_{\theta}(\tau_b))} $$

where \(R_{\theta}(\tau) = \sum_{t=1}^{T} R_{\theta}(s_t, a_t)\) is the human’s evaluation of the trajectory’s cumulative reward. In other words, we assume the human evaluator’s preference for a trajectory is proportional to the exponential of its reward.

We will incorporate Bayesian Theory of Mind into RLHF using a different choice model. Instead of making choices based on reward, we will model these choices based on how likely the trajectories would have been generated if the human evaluators were to act in their own mental model of the world.

This set up makes the most sense in settings with well separated notion of dynamics and policy (i.e., not language). For example, in robotics settings, where the environment is the physical environment and the policy generates control inputs, there is little reason to think that humans will have a perfect model of physics.

Let’s denote the human evaluator’s mental model as \(\hat{P}_{\theta}(\tau)\). For example, for the MDP process, \(\hat{P}_{\theta}(\tau) = \prod_{t=1}^{T}\hat{P}_{\theta}(s_t|s_{t-1}, a_{t-1})\hat{\pi}_{\theta}(a_t|s_t)\). We can model the above intuition using the following choice model:

$$ \begin{align} P(c=\tau_a|x; \theta) &= \frac{\exp(\log \hat{P}_{\theta}(\tau_a))}{\exp(\log \hat{P}_{\theta}(\tau_a)) + \exp(\log \hat{P}_{\theta}(\tau_b))}\\ &= \frac{\hat{P}_{\theta}(\tau_a)}{\hat{P}_{\theta}(\tau_a) + \hat{P}_{\theta}(\tau_b)} \end{align} $$

where we have replaced reward with the log likelihood of trajectories.

Similar to the reward-based choice model, we estimate the model parameters \(\theta\) by maxmizing model log likelihood on collected human evaluator choices:

$$ \begin{align} L(\theta) &= \log P(c=\tau_a|x; \theta) \\ &= \log \hat{P}_{\theta}(\tau_a) - \log \left(\exp(\log \hat{P}_{\theta}(\tau_a)) + \exp(\log \hat{P}_{\theta}(\tau_a))\right) \end{align} $$

Here we are considering a simplifed setting where we have observed only a single choice.

This log likelihood looks rather complex. Let’s analyze its behavior by computing its gradient:

$$ \begin{align} \nabla_{\theta}L(\theta) &= \nabla_{\theta}\log \hat{P}_{\theta}(\tau_a) - \mathbb{E}_{\overline{P}(c=\tau|x, \theta)}\left[\nabla_{\theta}\log \hat{P}_{\theta}(\tau)\right] \\ &= \nabla_{\theta}\log \hat{P}_{\theta}(\tau_a) - \left[\overline{P}(c=\tau_a|x; \theta)\nabla_{\theta}\log \hat{P}_{\theta}(\tau_a) + \overline{P}(c=\tau_b|x; \theta)\nabla_{\theta}\log \hat{P}_{\theta}(\tau_b)\right] \\ &= \overline{P}(c=\tau_b|x; \theta)\left[\nabla_{\theta}\log \hat{P}_{\theta}(\tau_a) - \nabla_{\theta}\log \hat{P}_{\theta}(\tau_b)\right] \end{align} $$

where the overline \(\overline{P}\) denotes stop gradient. Here, \(\overline{P}(c|x; \theta)\) is the model’s current choice over the two trajectories.

We see that, in general, if \(\tau_a\) is selected as the better one, then the model would maximize the likelihood of \(\tau_a\), with respect to both \(R_{\theta}\) and \(\hat{P}_{\theta}\), and minimize the likelihood of \(\tau_b\). However, such an opposite maximum likelihood estimation problem is weighted by the current probability of choosing the undesired trajectory. Assuming in the beginning of the optimization process, the model has no preference and thus the choice probability on the two trajectories are evenly divided, then we are simply multiplying the opposite maximum likelihood problem by a factor of 0.5. On the opposite end, let’s assume that the model has learned to strongly prefer \(\tau_a\) towards the end of the optimization process, then there are two consequences. The log likelihood of \(\tau_b\) under the model should be very small, and the model’s probability for choosing \(\tau_b\) should also be very small. In this case, the model stop optimizing for anything, because of the zero-weighting in front.

I haven’t thought deeply about whether this formulation could lead to any degeneracy, which strangely feels like it will since the model will hardly get any meaningful gradients in the beginning of the optimization process (but this problem will usually get solve by randomized algorithms). Nevertheless, there are some immediate benefits. By transforming maximum likelihood estimation of the choice model into maximum likelihood estimation of the preferred trajectory, we have turned the RLHF problem into the familiar IRL and Bayesian Theory of Mind problem. In other words, we have identified a method to select pseudo “expert” trajectories among randomly generated trajectories in an adaptive manner; but rather than blindly optimizing for any pseudo expert trajectories during a single iteration, since they are not yet optimal in the beginning of training, we co-evolve the joint human-RL system. We can now integrate all of the advances of model-based RL, IRL, and hierarchical Bayesian models into the RLHF pipeline to find more robust and generalizable reward.